Acerca da amostragem estratificada, analise as afirmativas a seguir.
I. Visa a produzir estimativas mais precisas, produzir estimativas para a população toda e para subpopulações.
II. Em geral, quanto menos os elementos de cada estrato forem parecidos entre si e também entre os estratos, maior será a precisão dos estimadores.
III. A estratificação produz necessariamente estimativas mais eficientes do que a amostragem aleatória simples.
Está correto o que se afirma em
A Receita Federal do Brasil e a Secretaria Municipal de Fazenda, hipoteticamente, celebram convênio para compartilhamento de informações sujeitas a sigilo fiscal da declaração anual de imposto de renda. Sob os termos do convênio, é obrigatória a solicitação individualizada e motivada do dado a que se deseja ter acesso e haverá custo para sua disponibilização, uma vez que o serviço que assegura os termos do convênio é prestado com exclusividade pelo Serpro, de acordo com tabela de preços por ele praticada. Após o levantamento da base de dados de lançamentos fiscais do ITBI dos últimos cinco anos junto ao sistema da Secretaria de Fazenda, a Municipalidade avalia a possibilidade de confrontar tais registros com os imóveis declarados anualmente pelos proprietários à Fazenda Federal. Os custos de obtenção e análise de todos os dados do IRPF, entretanto, pareceram proibitivos. Na circunstância narrada,
Uma amostra aleatória simples
Y1, Y2,..., Yn, retirada de uma população Bernoulli, é tal que
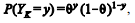
para
y = 0 ou 1, 0 < θ < 1 e k = 1, 2, ..., n. O objetivo é efetuar inferências acerca do parâmetro θ mediante aplicação de métodos computacionais.
Considerando que para
, 
represente a estimativa de θ obtida na r-ésima iteração de um algoritmo de estimação, julgue o seguinte item.
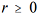
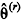
O amostrador de Gibbs, um algoritmo sequencial de Monte Carlo, permite simular a distribuição a priori do parâmetro θ, desde que a forma funcional da sua função de densidade, ƒ(θ), seja conhecida.
Considere uma amostragem aleatória simples de uma população de tamanho muito grande. O tamanho aproximado da amostra que permite estimar uma proporção Y, com margem de erro máxima de 0,05, a um nível de confiança de 90%, é
Em estudos numéricos, somente as amostragens probabilísticas permitem a correta generalização para a população dos resultados amostrais. Considerando essa informação, assinale a alternativa correta.
Suponha que uma amostra de tamanho n = 6 será extraída de uma população de 20 indivíduos, sendo a idade a variável de interesse. A população é mostrada na íntegra a seguir.
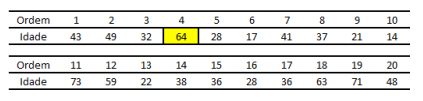
A extração seguirá a técnica de amostragem sistemática, iniciando pelo indivíduo de ordem 4, acima grifado.
Se o intervalo de seleção é igual a três, a estimativa não tendenciosa da média populacional será igual a:
Os tempos de duração de exames de cateterismo cardíaco ( Y, em minutos) efetuados por determinada equipe médica seguem uma distribuição normal com média µ e desvio padrão σ, ambos desconhecidos. Em uma amostra aleatória simples de 16 tempos de duração desse tipo de exame, observou-se tempo médio amostral igual a 58 minutos, e desvio padrão amostral igual a 4 minutos.
A partir da situação hipotética apresentada e considerando Φ(2) = 0,977, em que Φ(z) representa a função de distribuição acumulada de uma distribuição normal padrão e z é um desvio padronizado, julgue o item que se segue, com relação ao teste de hipóteses H0 = µ ≥ 60 minutos, contra HA = µ < 60 minutos, em que H0 e HA denotam, respectivamente, as hipóteses nula e alternativa.
Nesse teste de hipóteses, comete-se o erro do tipo II caso a hipótese H0 seja rejeitada, quando, na verdade, H0 não deveria ser rejeitada.
X1, X2, ..., X10 representa uma amostra aleatória simples retirada de uma distribuição normal com média µ e variância σ2, ambas desconhecidas. Considerando que 
e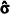 
representam os respectivos estimadores de máxima verossimilhança desses parâmetros populacionais, julgue o item subsecutivo.
A soma X1 + X2 + ... + X10 é uma estatística suficiente para a estimação do parâmetro μ.
Analise a tabela de distribuição de frequência abaixo:
TABELA: anos de serviço na PM, militares do 185º BPM, dezembro de 2017:
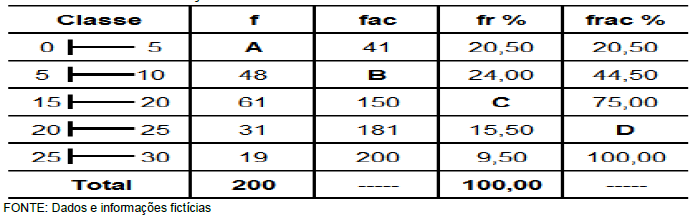
Sabe-se que f é a frequência absoluta, fac é a frequência absoluta acumulada, fr% é a frequência relativa (percentual) e frac% é a frequência relativa (percentual) acumulada. Considerando as informações da tabela, é CORRETO afirmar que os valores de A, B, C, D, são respectivamente:
Para o planejamento de uma pesquisa de campo, do ponto de vista estatístico, existem três aspectos fundamentais a definir, quais sejam: a população alvo, o modo de seleção e o tamanho da amostra.
Esses aspectos estão logicamente interligados e sobre eles é correto afirmar que:
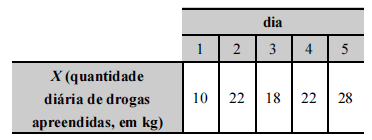
Tendo em vista que, diariamente, a Polícia Federal apreende uma quantidade X, em kg, de drogas em determinado aeroporto do Brasil, e considerando os dados hipotéticos da tabela precedente, que apresenta os valores observados da variável X em uma amostra aleatória de 5 dias de apreensões no citado aeroporto, julgue o próximo item.
A tabela em questão descreve a distribuição de frequências da quantidade de drogas apreendidas nos cinco dias que constituem a amostra.
De acordo com a NBC TA 520, assinale a alternativa que se caracteriza como um procedimento analítico substantivo.
Uma amostra aleatória simples
Y1, Y2,..., Yn, retirada de uma população Bernoulli, é tal que
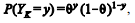
para
y = 0 ou 1, 0 < θ < 1 e k = 1, 2, ..., n. O objetivo é efetuar inferências acerca do parâmetro θ mediante aplicação de métodos computacionais.
Considerando que para
, represente a estimativa de θ obtida na r-ésima iteração de um algoritmo de estimação, julgue o seguinte item.
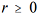
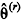
No algoritmo de Metropolis-Hastings tem-se a forma iterativa
, na qual ƒ representa a função de densidade a priori de θ, e 
> 0 representa um incremento aleatório. Nesse algoritmo, a probabilidade de aceitação do valor proposto 
como uma estimativa viável para o parâmetro de interesse é constante.
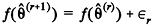
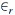
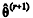
A respeito de um plano amostral com base na amostragem por conglomerados, assinale a alternativa correta.
Para obter uma amostra de tamanho 1.000 dentre uma população de tamanho 20.000, organizada em um cadastro em que cada elemento está numerado sequencialmente de 1 a 20.000, um pesquisador utilizou o seguinte procedimento:
I - calculou um intervalo de seleção da amostra, dividindo o total da população pelo tamanho da amostra: 20.000/1.000 = 20;
II - sorteou aleatoriamente um número inteiro, do intervalo [1, 20]. O número sorteado foi 15; desse modo, o primeiro elemento selecionado é o 15º;
III - a partir desse ponto, aplica-se o intervalo de seleção da amostra: o segundo elemento selecionado é o 35º (15+20), o terceiro é o 55º (15+40), o quarto é o 75º (15+60), e assim sucessivamente.
O último elemento selecionado nessa amostra é o
