Considere a amostra aleatória de tamanho n = 4, [20, 25, 24, 22], obtida de uma distribuição N(µ, σ2).
Nesse caso, as estimativas UMVU (Estimador não viciado de variância uniformemente mínima) e EMV (Estimador de Máxima Verossimilhança) dos parâmetros µ e σ 2 são, respectivamente:
Uma variável aleatória X tem função geradora de momentos dada por:
mx ( t ) =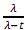 
, para t < λ
O valor de E(X2) é:
Um hospital está preocupado com a quantidade de atendimento aos acidentados de trabalho. Sabe-se que o tempo do atendimento dos acidentes de trabalho tem uma distribuição normal com desvio padrão de 24 horas/homens por semana. Para uma analise detalhada, tomou-se uma amostra de 16 hospitais e observaram-se, para essa amostra, os seguintes números de horas/homem atendidos nos acidentes de trabalho:
15; 4; 5; 19; 17; 16; 4; 14; 16; 20; 18; 8; 7; 5; 8; 16.
Construa um intervalo de confiança para o número médio de horas/homem para o atendimento de acidentes de trabalho. Responda, considerando o intervalo, se é necessário preocuparse, sabendo que o hospital pode atender 1hora/homens semanal nos acidentes de trabalho.
Dado: Use coeficiente de confiança de 95% cujo valor equivale 1,96.
Marque a alternativa CORRETA.
Em determinada pesquisa sobre o consumo de três produtos, A, B e C, verificou-se que:
25 pessoas consomem o produto A.
8 pessoas consomem os produtos A e B.
13 pessoas consomem os produtos C e B.
22 pessoas consomem o produto B.
18 pessoas consomem os produtos A e C.
32 pessoas consomem o produto C.
5 pessoas consomem os três produtos.
Nenhum dos três produtos é consumido por 17 pessoas.
Nessas condições, podemos afirmar que o número de pessoas pesquisadas é igual a:
Um estatístico deseja relacionar uma variável Y com duas outras variáveis que explicariam o valor de Y. São elas: X1 e X2. O modelo a ser ajustado é Y = ß0 + ß1X1 + ß2X2 + ε . Fixando valores para X1 e X2, observou os valores de Y e montou a seguinte tabela com os dados obtidos no experimento: 
Para suas análises econômicas e sociais, um pesquisador necessita ter uma estimativa da renda média familiar de uma população composta de 10 mil famílias. Com a finalidade de atender às necessidades do pesquisador, uma pesquisa de campo será realizada e uma amostra aleatória simples será delineada e selecionada, sem reposição. Uma das exigências do pesquisador é que a estimativa a ser realizada, através da média amostral, difira da verdadeira média em, no máximo, R$ 20,00, e que isso ocorra com probabilidade de 95%. Assumindo-se que o desvio padrão da renda familiar seja de R$ 200,00, o tamanho da amostra necessário para atender às exigências do pesquisador, no mínimo, deverá ser
Sejam X e Y variáveis aleatórias com densidade de probabilidade conjunta dada por:
f(x, y) = (x + y), se 0 < x < 1 e 0 < y < 1
0 nos demais caso
A probabilidade conjunta de que X seja menor do que 0,5 e Y seja menor do que 0,6 é:
Em um local público de atendimento existe um painel eletrônico com 231 números para atendimento. Com apenas um recepcionista, consegue atender até a posição do quartil um (Q1). Marque a alternativa CORRETA que representa a série da sequência dos clientes que foram atendidos.
