A função geradora de momentos M(t ) de uma variável aleatória X é definida para todos os valores reais de t como M(t )=E[etx]. Assinale a função geradora de momentos da distribuição Normal com média 0 e desvio-padrão 1.
Considerando fx(x ) a função densidade de probabilidade de uma variável aleatória X, analise as afirmativas a seguir.

Está(ão) correta(s) apenas a(s) afirmativa(s)
Sobre Modelos Lineares Generalizados (MLG), analise as afirmativas, marque V para as verdadeiras e F para as falsas.

A sequência está correta em
Um pesquisador deseja verificar se a quantidade de nascimentos do hospital em que trabalha segue uma distribuição
uniforme ao longo da semana. Para verificar sua hipótese, ele coletou o dia da semana de cada criança que nasceu no
hospital nas últimas 8 semanas. Analise a Tabela 1 com os dados a seguir.

Assinale a alternativa que contém o valor da estatística
Considerando os valores quantitativos emparelhados x e y de uma amostra aleatória com observações
independentes, analise as afirmativas a seguir, marque V para as verdadeiras e F para as falsas.
( ) O coeficiente de correlação linear mede a intensidade da relação linear entre x e y.
( ) Se existe correlação linear entre x e y, pode-se concluir que x causa y ou y causa x.
( ) Pode existir uma relação entre x e y mesmo quando a correlação linear é próxima de 0.
A sequência está correta em

Sobre propriedades dos estimadores pontuais, assinale a afirmativa INCORRETA.
As notas em uma prova de matemática dos alunos de uma determinada escola estão resumidas no seguinte gráfico Boxplot. Analise-o.
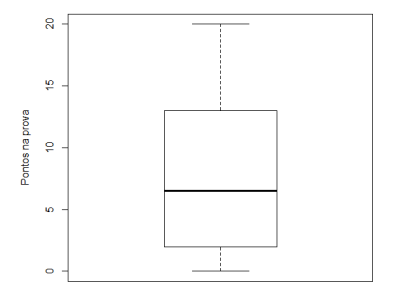
Sabendo que a prova valia 20 pontos, pode-se afirmar que
Um prefeito acredita que os habitantes de seu município estão lendo pouco, pois a biblioteca municipal está sempre
com pouco movimento. Para mudar essa situação, ele pensou em fazer uma campanha para estimular a leitura,
entretanto precisa comprovar estatisticamente que a média de livros lidos por habitante do município está abaixo da
média nacional para conseguir a liberação da verba para executar a campanha.
Informações adicionais
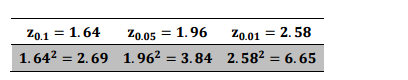
Qual o tamanho da amostra que o prefeito precisa coletar usando amostragem aleatória simples se ele deseja ter
90% de confiança e margem de erro 1, sabendo através de um estudo prévio que σ2
Com respeito à Inferência Bayesiana, analise as afirmativas a seguir.
I. O ideal quando se tem pouca informação inicial sobre um parâmetro θ é utilizar uma distribuição a priori p(θ) muito
informativa.
II. A distribuição a priori traz de maneira resumida a informação contida nos dados amostrais.
III. A distribuição a priori sempre influencia mais na distribuição a posteriori que os dados amostrais.
Está(ão) INCORRETA(S ) a(s) afirmativa(s)
Certo exame de sangue é capaz de detectar uma doença em 95% dos pacientes que estão doentes de fato. Além disso, ele detecta, erroneamente, a doença em 3% das pessoas saudáveis que fazem o exame (“falso positivo”). Sabendo que a doença atinge 5% da população, qual a probabilidade de uma pessoa estar doente dado que o exame detectou a doença?
O SAC de uma empresa recebe uma ligação a cada 20s. Qual a probabilidade de que em um minuto ele receba
exatamente duas ligações, sabendo que as ligações ocorrem de maneira independente uma das outras?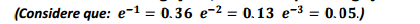
Sobre as técnicas de amostragem, assinale a afirmativa correta.
Calcule o valor de c para que f(x,y) seja uma função de densidade de probabilidade conjunta de X e Y.
Depois calcule a função de densidade de probabilidade condicional de X dado Y = y, em que 0 < y < 2 . Assinale a
alternativa que apresenta o valor de c e a função de densidade de probabilidade condicional pedida.
Para estudar o peso dos peixes de um tanque, foi feito um estudo amostral e coletado uma amostra aleatória de 10 peixes. Os pesos em kg dos peixes são mostrados a seguir: 5 4 3 3 6 7 7 2 8 5 Qual o Coeficiente de Variação (CV) do peso dos peixes da amostra retirada desse tanque?

