Questões de Concurso – Aprova Concursos

1)

Q270098 - CESGRANRIO - 2014 - EPE - Analista de Pesquisa Energética - Planejamento da Geração de Energia

Considere as informações a seguir para responder às questões de n ^os 57 a 60.

Considere o problema abaixo de Programação Linear: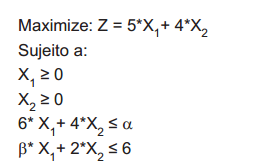

Considere que β= 1.
Qual o valor mínimo que α pode assumir para que a base ótima para o problema de programação linear apresentado permaneça a mesma encontrada quando α= 24?

a)
12
b)
14
c)
18
d)
20
e)
24

2)

Q270097 - CESGRANRIO - 2014 - EPE - Analista de Pesquisa Energética - Planejamento da Geração de Energia

Considere as informações a seguir para responder às questões de n ^os 57 a 60.

Considere o problema abaixo de Programação Linear: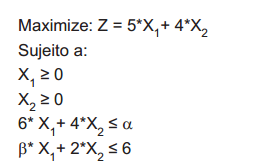

Considere que β= 1.
Qual é o valor máximo que α pode assumir para que a base ótima para o problema de programação linear apresentado permaneça a mesma encontrada quando α= 24?

a)
24
b)
30
c)
36
d)
40
e)
44

3)

Q270096 - CESGRANRIO - 2014 - EPE - Analista de Pesquisa Energética - Planejamento da Geração de Energia

Considere as informações a seguir para responder às questões de n ^os 57 a 60.

Considere o problema abaixo de Programação Linear: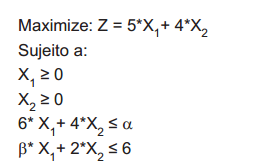

Sendo α = 24 e β = 1, o valor ótimo da função objetivo é:

a)
15
b)
20
c)
21
d)
24
e)
32

4)

Q270090 - CESGRANRIO - 2014 - EPE - Analista de Pesquisa Energética - Planejamento da Geração de Energia

Seja X uma variável aleatória contínua com função de densidade dada por 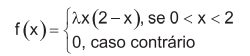com λ > 0 uma constante.

Qual é o valor da constante?

a)
λ = 1/4
b)
λ = 1/2
c)
λ = 3/4
d)
λ = 1
e)
λ = 2

5)

Q270095 - CESGRANRIO - 2014 - EPE - Analista de Pesquisa Energética - Planejamento da Geração de Energia

Considere as informações a seguir para responder às questões de n ^os 57 a 60.

Considere o problema abaixo de Programação Linear: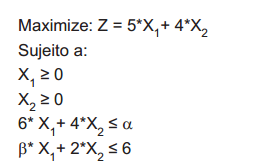

Considerando-se que α= 24, para qual valor de β o problema apresenta soluções múltiplas?

a)
-5/2
b)
0
c)
5/4
d)
5/2
e)
1

6)

Q270082 - CESGRANRIO - 2014 - EPE - Analista de Pesquisa Energética - Planejamento da Geração de Energia

A curva intensidade-duração-frequência (IDF) é obtida a partir da análise estatística de uma série longa de dados. Alternativamente, a intensidade de uma chuva (mm/h), em função do seu tempo de retorno em anos (TR) e da sua duração em minutos (t_d ), pode ser dada pela equação a seguir:

Em determinada localidade na região Sul do Brasil, obteve-se: a =625; b =0,25; c =20 e d =0,75. Para uma chuva com 5 min de duração e um tempo de retorno de 25 anos, portanto, a equação aponta uma intensidade, em mm/h, de

a)
100
b)
125
c)
150
d)
225
e)
625

7)

Q270094 - CESGRANRIO - 2014 - EPE - Analista de Pesquisa Energética - Planejamento da Geração de Energia

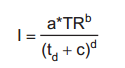
Considere as informações a seguir para responder às questões de n ^os 55 e 56.

Um feirante possui uma Kombi para transportar caixas de frutas. Em uma viagem, ele consegue transportar no veículo 200 caixas de laranjas - caso transporte apenas laranjas - ou 300 caixas de tangerinas - caso transporte apenas tangerinas. O lucro por caixa de frutas é o seguinte: 20 unidades monetárias pelas laranjas, 30 unidades monetárias pelas tangerinas e 35 unidades monetárias pelas maçãs. De acordo com sua estimativa de vendas, o feirante decide transportar pelo menos 100 unidades de maçãs. Considere a variá- vel X ₁ como a quantidade vendida de caixas de maçãs, X₂ a de caixas de laranjas e X ₃ a de caixas de tangerinas.

Um método utilizado para resolver esse tipo de problema de programação linear inteira é o

a)
simplex
b)
algoritmo de plano de corte
c)
gradiente conjugado
d)
de otimização recursiva
e)
das duas fases

Questões de Concurso – Aprova Concursos

Milhares de questões com o conteúdo atualizado para você praticar e chegar ao dia da prova preparado!