Considere duas sequências (A e B) de quatro termos cada, sendo ambas crescentes e de primeiro termo valendo 1. Sabe-se que A é uma progressão aritmética e B é uma progressão geométrica, assim como Sa é a soma dos quatro elementos de A e Sb é a soma dos quatro elementos de B. Se r é a razão da sequência A, q é a razão da sequência 
calcule o produto r· q.
Com relação a uma sequência numérica α1, α2, …, αn, julgue o item subsequente.
Considere que a sequência seja formada pelos seguintes termos, nessa ordem: 10, 12, 15, 19, 24, 30, 37. Nesse caso, a sequência numérica bj = αj + 1 - αj, em que j = 1, 2, …, 6 forma uma progressão aritmética.
Com relação a uma sequência numérica a 1, a2, …, an, julgue o item subsequente.
Se a sequência for uma sequência de Fibonacci, em que a1 = 4 e a2 = 9, então a6 = 57.
Sabendo que no primeiro dia de treino um Bombeiro percorreu 3 km e a cada dia seguinte percorria 200m a mais que no dia anterior, quantos quilômetros esse Bombeiro teria percorrido em 15 dias de treino?
Uma casa foi construída de tal forma que o número de azulejos presentes em cada cômodo forma uma progressão aritmética. Sabe-se que a soma e a diferença do número de azulejos dos cômodos que possuem a maior e a menor quantidade de azulejos são 385 e 165, respectivamente, e que o número de azulejos do cômodo com a segunda maior quantidade de azulejos é 260 . Assim, o número total de azulejos nessa casa é:
Progressões geométricas são sequências de números nas quais o próximo número é obtido a partir da multiplicação do número anterior por um número fixo, a razão. Sabendo que o terceiro número dessa progressão é 15 e o quinto é 135, qual das alternativas pode representar o segundo termo dessa razão?
Em uma progressão aritmética do tipo an sabe-se que a8/a4 = 6 e que o valor do 6º termo é igual a 7. Qual o valor do 10° termo?
Considere as seguintes situações: I.Correção de um capital inicial A, durante um ano, mês a mês, de 2% cada mês, efetuada sempre com base no capital do mês anterior. II.Acréscimo sobre um capital inicial B, durante um ano, mês a mês, de 2% de B, a cada mês. III.Retirada de um valor fixo X, mês a mês, durante um ano, de um capital inicial C. As situações I, II e III estão, respectivamente, associadas aos conceitos de progressões
Seja X a soma dos cinco primeiros termos de uma Progressão Aritmética (PA) e Y a soma do sexto ao décimo termos dessa progressão. Sabendo-se que Y-X=100, a razão da PA vale:
Uma sequência de números reais tem seu termo geral, an , dado por an = 4.23n+1, para n ≥ 1 Essa sequência é uma progressão
Em um país imaginário, o mandato presidencial dura 7 anos. Nesse país houve eleições para presidente no ano 2000, no ano 2007, haverá neste ano de 2014, e assim por diante. Após o ano de 2500, haverá eleições para presidente, pela primeira vez, no ano:
Ana e Bia são vendedoras de uma mesma loja. Em certo dia, Ana fez 4 vendas nos valores a1 , a2 , a3 e a4 , e Bia fez 5 vendas nos valores b1 , b2 , b3 , b4 e b5 . Considere x e y números reais tais que (x, a1 , a2 , a3 , a4 , y) e (x, b1 , b2 , b3 , b4 , b5 , y) formam progressões aritméticas.
Nessas condições, a fração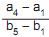 
é igual a
O termo geral de uma sequência de números reais (xn) para n ≥ 1 é dado por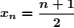 
.
Considere a sequência (yn) = (2xn ).
Em relação a essas duas sequências, assinale a alternativa correta
