Assinale a opção que completa de forma correta o seguinte caso:
"Um casal deseja saber qual é a formulação atuarial relativa à probabilidade de que apenas um dos componentes do casal esteja vivo, após os 25 anos seguintes."
Para o texto abaixo, indique a opção que completa de forma correta.
"A precifi cação do seguro toma por base duas fi guras básicas, sendo uma o risco, cuja medida é dada pela sua respectiva probabilidade - p(x), e pelo valor do dano, representada por Q. Sabe-se que p(x) varia entre zero e um, devendo ficar no intervalo aberto entre estes limites e que Q deve ser positivo. Dentro destas figuras básicas e inerentes às operações de seguro, para o segurado a recomendação mais adequada é de priorizar a efetivação dos seguros para os casos em que tenham . . .".
Um estudo de L. Y. Wang et al., publicado no Journal
of Adolescent Health, em 2008, estabeleceu uma relação entre
o índice de massa corporal (x) de uma pessoa na adolescência e
a probabilidade de essa pessoa tornar-se obesa quando adulta, por
meio de um modelo de regressão não-linear na forma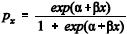
, em que 
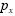representa a probabilidade
esperada de uma pessoa tornar-se obesa na fase adulta, dado que,
na adolescência, a massa corporal era igual a um valor x, e ? e ?
são coeficientes do modelo. Segundo os autores do estudo,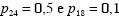
.
Com base nessas informações, julgue os itens de 108 a 110.
Do ponto de vista de modelos lineares generalizados, a função de ligação para o modelo apresentado é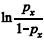
.
Um plano de benefícios adota o modelo bidecremental, em
que os decrementos constituem morte e invalidez. Nesse plano, a
probabilidade de morte aos 51 anos de idade é igual a 0,02 e a
probabilidade de entrada em invalidez aos 51 anos é igual a 0,003.
Com relação ao plano de benefícios mencionado acima, julgue os itens
subseqüentes.
A probabilidade de o indivíduo ativo e válido de 51 anos de idade chegar aos 52 anos de idade nessa mesma condição é maior que 0,9.
Com base nas informações do texto, julgue os itens subseqüentes.
A auto-correlação parcial entre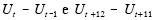 
é igual a 
.
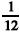Um plano de benefícios adota o modelo bidecremental, em
que os decrementos constituem morte e invalidez. Nesse plano, a
probabilidade de morte aos 51 anos de idade é igual a 0,02 e a
probabilidade de entrada em invalidez aos 51 anos é igual a 0,003.
Com relação ao plano de benefícios mencionado acima, julgue os itens
subseqüentes.
A probabilidade de uma pessoa viva e ativa de 51 anos de idade morrer aos 52 anos de idade corresponde a 0,017.
Um estudo de L. Y. Wang et al., publicado no Journal
of Adolescent Health, em 2008, estabeleceu uma relação entre
o índice de massa corporal (x) de uma pessoa na adolescência e
a probabilidade de essa pessoa tornar-se obesa quando adulta, por
meio de um modelo de regressão não-linear na forma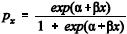
, em que 
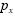representa a probabilidade
esperada de uma pessoa tornar-se obesa na fase adulta, dado que,
na adolescência, a massa corporal era igual a um valor x, e ? e ?
são coeficientes do modelo. Segundo os autores do estudo,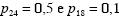
.
Com base nessas informações, julgue os itens de 108 a 110.
Segundo esse estudo, a probabilidade de uma pessoa tornar-se obesa na fase adulta, quando sua massa corporal na adolescência for igual a x, será igual, em média, a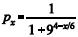
.
Um estudo de L. Y. Wang et al., publicado no Journal
of Adolescent Health, em 2008, estabeleceu uma relação entre
o índice de massa corporal (x) de uma pessoa na adolescência e
a probabilidade de essa pessoa tornar-se obesa quando adulta, por
meio de um modelo de regressão não-linear na forma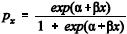
, em que 
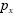representa a probabilidade
esperada de uma pessoa tornar-se obesa na fase adulta, dado que,
na adolescência, a massa corporal era igual a um valor x, e ? e ?
são coeficientes do modelo. Segundo os autores do estudo,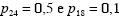
.
Com base nessas informações, julgue os itens de 108 a 110.
A estimação dos coeficientes pode ser feita via máxima verossimilhança, e a estatística de Hosmer-Lemeshow é útil para a verificação da qualidade do ajustamento. Uma avaliação da significância estatística das estimativas encontradas para os coeficientes ? e ? pode ser feita pelo teste de Wald ou pelo teste da razão de verossimilhança.
