Relacione as características dos diferentes processos de medição da rugosidade de superfícies às suas respectivas designações.
1- Os riscos superficiais inerentes ao processo de medição não alteram muito seu valor.
2- Em perfis de rugosidade periódicos, define muito bem a superfície.
3- Desconsidera picos e vales que não sejam representativos da superfície.
( ) Rugosidade média, Ra
( ) Rugosidade média, Rz
( ) Rugosidade média do terceiro pico e vale, R3z
Assinale a opção que indica a relação correta, segundo a ordem apresentada.
Em um dado instante, o rolete A apresenta a velocidade indicada na figura a seguir.
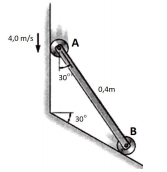
Nesse mesmo instante, a velocidade no rolete B vale
A figura a seguir apresenta, esquematicamente, uma broca do tipo W.
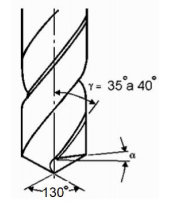
Essa broca é adequada para furar peças constituídas por
A figura a seguir ilustra um gráfico conhecido como “curva da banheira".
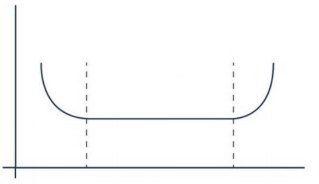
Em relação à manutenção de um componente, esta curva indica o seu comportamento característico quanto
Uma tora de madeira de seção retangular de lados 50 cm e 40 cm e comprimento de 4 metros flutua na superfície d´água.
Sabendo-se que o peso específico da água é de 1kg/dm3, a densidade da madeira é de 0,60, e que sobre a tora de madeira equilibra-se um corpo de massa 100kg, o percentual de volume da tora de madeira que estará submerso é de
A difusividade térmica pode ser considerada como sendo
Um sistema de refrigeração consiste na retirada de calor de um ambiente ou produto. Ao ser admitido no condensador, o fluido refrigerante no estado gasoso deve ser condensado antes de retornar ao evaporador. Este processo se dá através de um trocador de calor, denominado condensador, por meio de três fases distintas, que ocorrem na seguinte ordem:
Assinale a opção que indica, em engenharia de manutenção, o conceito de manutenabilidade.
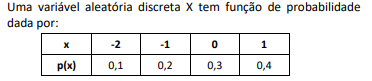
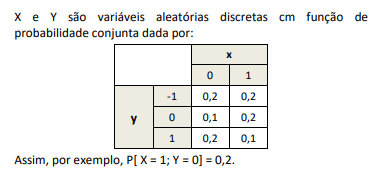
Se F(x) representa a função de distribuição de X, ∀ x real, então F(-0,8) é igual a
Considere que uma amostra aleatória simples de tamanho 100 de uma distribuição Poisson com parâmetro λ = 4 será observada.
Com base no teorema do limite central, a probabilidade de que a média amostral seja maior do que 4,5 é, aproximadamente, igual a
Avalie se as afirmativas a seguir, relacionadas à estimação por máxima verossimilhança de um parâmetro θ, são falsas ou verdadeiras.
( ) A função de verossimilhança de um conjunto de variáveis aleatórias é definida como a função de densidade (ou de probabilidade) conjunta dessas variáveis olhada como função de θ.
( ) Se X1, X2, ..., Xn é uma amostra aleatória simples de uma densidade uniforme no intervalo (0, θ), o estimador de máxima verossimilhança de θ é máx{Xi}, ou seja, é a n-ésima estatística de ordem.
( ) Se X1, X2, ..., Xn é uma amostra aleatória simples de uma densidade N(µ, σ2), σ conhecida, o estimador de máxima verossimilhança de µ é a média amostral.
Na ordem apresentada, as afirmativas são, respectivamente,
Para testar a hipótese nula H0 de que a proporção populacional de pessoas acometidas por certa doença virótica não é maior do que 10% contra a hipótese alternativa de que ela é maior do que 10%, uma amostra aleatória simples de tamanho 256 foi observada e revelou que, dessas 256 pessoas, 32 estavam acometidas pela referida doença.
Usando a proporção de acometidos na amostra como estatística de teste e apoiado no teorema do limite central, o p-valor aproximado associado a esses dados e a respectiva decisão a ser tomada ao nível de significância de 5%, são
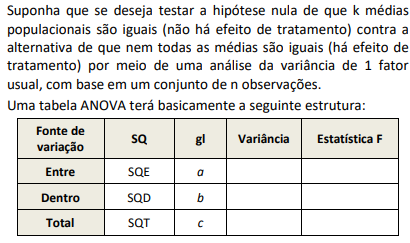
Obtidos corretamente os valores de SQE, SQD e SQT, o valor da estatística de teste F será dado por