A respeito de uma amostra de tamanho n = 10, com os valores amostrados {0,10, 0,06, 0,10, 0,12, 0,08, 0,10, 0,05, 0,15, 0,14, 0,11}, extraídos de determinada população, julgue os itens seguintes.
Para um teste Z ou t de Student bilateral (com pelo menos 9 graus de liberdade), uma estatística do teste menor que 1,5 é considerada não significativa para o nível de significância de 5%.
Em estudo acerca da situação do CNPJ das empresas de determinado município, as empresas que estavam com o CNPJ regular foram representadas por 1, ao passo que as com CNPJ irregular foram representadas por 0. Considerando que a amostra {0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1} foi extraída para realizar um teste de hipóteses, julgue os itens subsequentes.
Uma vez que a amostra é menor que 30, a estatística do teste
utilizada segue uma distribuição t de Student.
100 A estatística do teste para testar a hipótese H0: P = 0,5 contra
H1: P … 0,5, em que P representa a proporção de empresas cujo
CNPJ está regular, é maior que 2.
O livro Probabilidade e Estatística de Jay L. Devore, 2011, faz o seguinte relato sobre o valor P: “ O valor P
é a probabilidade calculada, assumindo-se que H0 seja verdadeira, de se obter um valor da estatística de teste
pelo menos tão contraditória a H0, quanto o valor que realmente resultou". Com base nesse relato, marque V
para as afirmativas verdadeiras e F para as falsas.
Assinale a sequência correta.
Em uma pesquisa realizada na empresa Alfa com 40 funcionários escolhidos aleatoriamente, com reposição, observou-se que
26apresentavam uma idade superior a 30 anos. Atribuiu-se 26 sinais positivos para os que apresentaram uma idade superior a
30anos e 14 sinais negativos para o restante (observação: nenhum funcionário apresentou a idade de 30 anos). Decide-se
aplicar o teste do sinal para averiguar se a proporção populacional de sinais positivos ( p) é igual a 50%, a um nível de
significância de 5%. Foram formuladas as hipóteses H0: p = 50% (hipótese nula) e H1: p ≠ 50% (hipótese alternativa). Com a
aproximação da distribuição binomial pela normal, sem a correção de continuidade, foi apurado o valor do escore reduzido k
correspondente para comparação com o valor crítico z da distribuição normal padrão ( Z) tal que P( |Z| ≤ z) = 95% . O valor de k é
tal que
Com relação a testes de hipóteses estatísticas e denominando H0 como sendo a hipótese nula e H1 a hipótese alternativa, a
definição de potência de um teste corresponde à probabilidade de
Para o mesmo caso, o vendedor ainda havia informado
que o desvio padrão do faturamento era de R$ 50,00 e
que isso era uma vantagem da empresa, pois a variabilidade
era pequena. Ao se fazer o teste H0: σ2 = 2500,
contra a hipótese H1: σ2 > 2500 com nível de significância
de 5%, é correto afirmar que o teste indicado é
Um pesquisador, desejando comprovar se dois grupos diferem em tendências centrais, decide utilizar o teste da mediana
formulando as hipóteses:
H0 : os dois grupos provêm de populações com a mesma mediana (hipótese nula).
H1 : a mediana de um grupo difere da mediana do outro grupo (hipótese alternativa).
Neste caso, o pesquisador
Durante uma semana, observa-se a quantidade de determinadas ocorrências, esperando que diariamente ocorram 20 destes
tipos de ocorrências. Para esta análise, foram levantados os seguintes dados em uma semana escolhida aleatoriamente:
qui-quadrado. Foram formuladas as hipóteses H0: as frequências são iguais em todos os dias da semana (hipótese nula) e H1:
as frequências são diferentes.
Observação: o valor crítico do qui-quadrado tabelado da distribuição qui-quadrado, ao nível de significância de α e com o respectivo número de
graus de liberdade do teste, apresentou um valor superior ao valor do qui-quadrado observado.
O valor do qui-quadrado observado é
O desvio padrão de uma população normal de tamanho infinito é desconhecido e deseja-se saber se a média μ desta população
é inferior a 17,5 a um nível de significância α. Foram formuladas as hipóteses H0: μ = 17,5 (hipótese nula) e H1: μ < 17,5
(hipótese alternativa). Uma amostra aleatória de tamanho 9 é extraída desta população, observando-se que a média amostral foi
igual a 15 e a soma dos quadrados de todos os elementos da amostra foi igual a 2.097. Considerando que tα o quantil da
distribuição t de Student para o teste unicaudal tal que a probabilidade P(t > tα) = α, com n graus de liberdade, tem-se com base
na amostra que H0
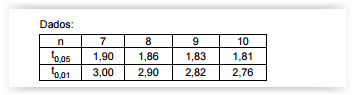
No teste de hipótese ao nível de 5% de significância para
verificar a linearidade (H0: β = 0 contra H1: β ≠ 0), o valor
crítico de F para se rejeitar H0 é, aproximadamente,
A variância de uma população normalmente distribuída e de tamanho infinito é desconhecida. Uma amostra aleatória de
tamanho 9 é extraída desta população obtendo-se a média dos elementos da amostra igual a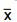 
e o respectivo desvio padrão
amostral igual a 2,7. Considere o objetivo de testar a hipótese H0: μ = 20 (hipótese nula) contra H1: μ ≠ 20 (hipótese alternativa),
ao nível de significância de 5%, com a realização do teste t de Student. Sabe-se que t0,025 corresponde ao quantil da distribuição
t de Student para o teste unicaudal tal que a probabilidade P(t > t0,025) = 0,025, com n graus de liberdade.
A hipótese H0 será rejeitada caso I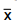 
Sobre teste de hipóteses, marque V para as afirmativas verdadeiras e F para as falsas. ( ) Comete-se o erro do tipo I, quando se rejeita uma hipótese nula verdadeira. ( ) O poder de um teste é a probabilidade da hipótese nula ser rejeitada, dado que ela é falsa. ( ) O valor p de um teste de hipótese é a probabilidade da hipótese nula ser rejeitada. ( ) O erro do tipo I é também chamado de nível de confiança de um teste de hipóteses. Assinale a sequência correta.
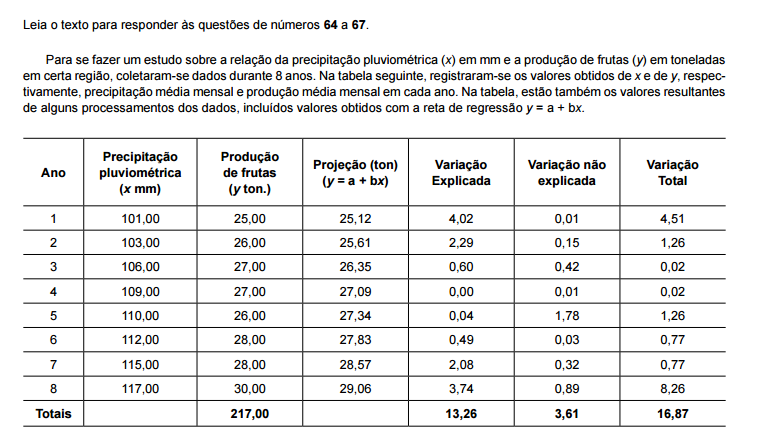
Para testar a eXistência da regressão, a um determinado nível de significância, optou-se pelo teste t de Student, em que foram formuladas as hipóteses H0: β = 0 (hipótese nula) e H1: β ≠ 0 (hipótese alternativa). Sabendo-se que o coeficiente de explicação (R2), definido como sendo o resultado da divisão da variação explicada pela variação total, é igual a 62,5%, tem-se que o valor do t calculado ( tc ) utilizado para comparação com o respectivo t tabelado é tal que
Um pesquisador desenvolve um estudo com uma população normal, considerada de tamanho infinito e desvio padrão populacional
igual a 65. Sendo μ a média da população, deseja executar o teste H0: μ = 70 (hipótese nula) contra H1: μ > 70 (hipótese
alternativa). Para isto, utiliza uma amostra aleatória de tamanho 400 com um nível de significância de 5%, considerando que na
curva normal padrão (Z ) as probabilidades P(Z > 1,64) = 0,050 e P(Z > 1,96) = 0,025. O pesquisador encontrou um valor para a
média amostra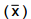 
sabendo-se que este valor é o maior valor tal que H0 não é rejeitada. O valor de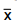 
Considere o experimento que consiste no lançamento de uma moeda quatro vezes. Para testar se a moeda é honesta, é feito um teste de hipóteses Ho: contra Ha: onde p é a proporção de caras. O critério de decisão estipula que se o número de caras for diferente de dois a hipótese nula deve ser rejeitada. Se, de fato, p = 0,25 a probabilidade de que o Erro do Tipo II seja cometido é:
