Para os circuitos de maratonas aquáticas realizadas em mares calmos e próximos à praia, é montado um sistema de boias que determinam o trajeto a ser seguido pelos nadadores. Uma das dificuldades desse tipo de circuito é compensar os efeitos da corrente marinha. O diagrama contém o circuito em que deve ser realizada uma volta no sentido anti-horário. As quatro boias estão numeradas de
1 a 4. Existe uma corrente marinha de velocidade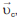 
, cujo módulo é 30 metros por minuto, paralela à praia em toda a área do circuito. Nas arestas mais longas, o nadador precisará nadar na direção apontada pelos vetores 
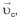dos pontos 1 até 2 e de 3 até 4. Considere que a velocidade do nadador é de 50 metros por minuto, em relação à água, durante todo o circuito.
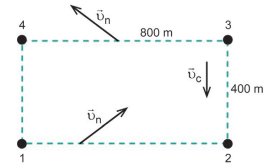
Nessa situação, em quantos minutos o nadador completará a prova?
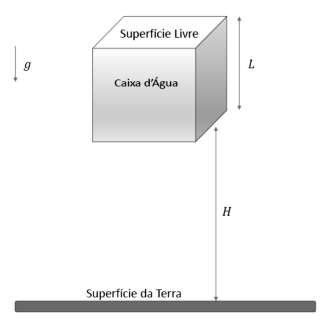
Na figura precedente, uma caixa d’agua cúbica de lado L, fixa em determinada altura H da superfície da terra, está completamente cheia com a superfície aberta (superfície livre) em contato com o ar, e a parede de baixo da caixa é perpendicular com a direção vertical. Considere que um pequeno orifício de área a seja aberto na parede de baixo da caixa e a água comece a vazar para o ar. Considere também que o regime de escoamento da água seja o de um fluido ideal, isto é, um fluido incompressível e não viscoso.
Com base nessas informações, e assumindo-se por g a aceleração da gravidade na superfície da terra, é correto afirmar que, imediatamente após a abertura do orifício na base da caixa, a velocidade inicial de queda V da superfície livre será dada por
Suponha que a cabine de um elevador tem 400 kg e dimensões correspondentes a 0,6 m x 1,0 m x 0,6 m (comprimento x largura x altura), já submersa em um tanque de água. Ao descer ainda mais, o elevador parte do repouso, e sua velocidade varia, de maneira linear, até atingir a marca de 1,5 m/s em 1,5 s. Considere o módulo do campo gravitacional local igual a 10 m/s², e a densidade da água igual a 1.000 kg/m³. Desconsiderando a viscosidade e o arrasto da água sobre o elevador, a tração sentida no cabo de aço que segura a cabine, durante esse intervalo de tempo, será igual a
Uma bola com intensidade de velocidade v e massa m cai verticalmente sobre um cano que, depois do choque, faz com que ela saia na horizontal com a mesma intensidade de velocidade. Considerando o módulo do campo gravitacional local igual a g e sabendo que o choque durou um instante bem pequeno t, é correto afirmar que o módulo da força média exercida pelo cano sobre a bola foi igual a
Considere o gráfico velocidade (v) x tempo (t) de uma bola em movimento sobre planos descentes, ascendentes ou sem inclinação. Qual das seguintes alternativas melhor expressa o movimento da bola de acordo com o gráfico?
Considere um objeto com massa m preso a um cabo ideal, e suponha duas situações. Na primeira situação, o objeto é levantado pelo cabo e percorre uma altura h com velocidade
constante. Na segunda situação, o mesmo objeto é levantado pelo cabo e percorre a mesma altura, porém a velocidade aumentou linearmente durante o percurso, com aceleração a. Admita o módulo do campo gravitacional g constante nessas situações e despreze a resistência do ar. Com base nesses dados, é correto afirmar que o trabalho W1 e W2, realizado através da força de tração do cabo, respectivamente, na primeira e na segunda situação, tem valor
A figura abaixo apresenta dois reservatórios de água distantes um do outro 2 m.
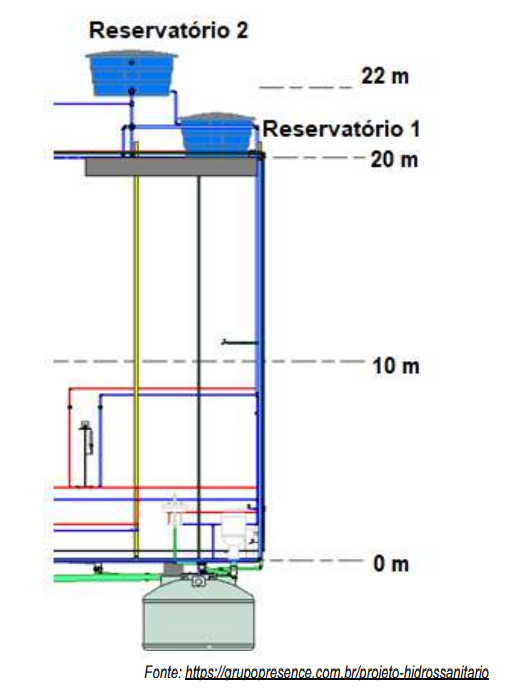
Sobre a velocidade de queda da água em cada reservatório é correto afirmar que:
De uma maneira geral e comum, posição, velocidade e aceleração de um corpo de dimensões desprezíveis são expressas através de vetores quando tratamos com movimento de translação. Essas grandezas possuem módulo, direção e sentido e obedecem a suas operações matemáticas de soma, subtração, produto escalar e vetorial. Em um caso bem particular de movimento retilíneo a notação vetorial pode ser deixada de lado, uma vez que o corpo pode se mover apenas no sentido positivo e negativo. De modo similar, um corpo rígido em rotação em torno de um eixo só pode girar nos sentidos horário ou anti-horário.
De uma maneira geral as grandezas angulares, deslocamentos infinitesimais, velocidade e aceleração, podem ser expressas por meio de notação vetorial?
Para o diagrama apresentado, as projeções nos planos A1, A2 e A3, indicadas pelas setas, referem-se às leis de Boyle, de Gay-Lussac e de Charles, respectivamente.
Um condutor deslocava-se pela Avenida X em um trecho que era constituído por pista simples, asfaltada, reta, plana, composta por duas faixas de trânsito de mesmo sentido de tráfego, separadas entre si por linha simples seccionada de cor branca. Ele trafegava pela faixa de trânsito direita a 72 km/h quando, em um dado momento, um pedestre, deslocando-se com velocidade constante de 5,4 km/h, proveniente da esquerda para a direita (considerando o sentido de deslocamento do veículo), entrou na referida avenida, momento em que o condutor percebeu o perigo e, visando evitar o atropelamento, reagiu e freou o seu veículo bruscamente até o repouso. Dados do telefone celular do condutor mostraram que a desaceleração média (considerada constante) do veículo foi de 7,975 m/s². Imagens de uma câmera de segurança, localizada nas proximidades, mostraram que o pedestre deslocou-se em trajetória perpendicular à pista.
Considerando-se que o tempo de percepção-reação do motorista foi de 1,0 s, que cada faixa de trânsito media 3,0 m de largura, que a largura do veículo era igual à largura da faixa, que ele ocupou apenas a faixa de trânsito direita durante todo seu movimento e que a distância entre o veículo e o pedestre era de 40 m quando o referido pedestre adentrou na pista, é correto afirmar que o atropelamento
Uma partícula com massa m e carga q move-se com uma velocidade v e entra em uma região de campo magnético uniforme B, como mostrado na figura a seguir. A partícula atinge a parede localizada a uma distância d da entrada da fenda. Se a velocidade da partícula permanece a mesma, mas sua razão carga-massa dobra, qual será a distância da fenda de entrada para a parede que receberá o impacto?
Uma corda homogênea está inicialmente em repouso na horizontal e tem sua extremidade esquerda presa em uma parede. Em dado instante, sua extremidade direita é posta para oscilar verticalmente e, dois segundos após o início das oscilações, o perfil da corda é o mostrado na figura.
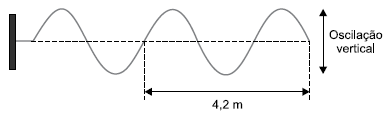
A velocidade de propagação das ondas nessa corda é de
As figuras a seguir ilustram, simplificadamente, o princípio de funcionamento de um GPS: três satélites, posicionados a distâncias R1, R2 e R3, emitem ondas eletromagnéticas que comunicam a receptores situados na superfície da Terra suas respectivas distâncias ao longo do tempo. Tais satélites perfazem duas voltas por dia na Terra, enquanto satélites geoestacionários demoram um dia para dar uma volta no nosso planeta.
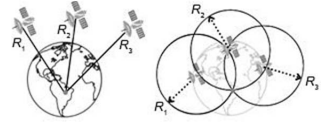
A partir das informações e das figuras apresentadas, julgue o seguinte item.
A partir das informações e das figuras apresentadas, julgue o seguinte item.
Considere que dois satélites, de massas m1 e m2, respectivamente, sendo m2 igual ao dobro de m1, estejam em órbita circular no mesmo planeta a uma mesma altitude, com velocidades v1 e v2, respectivamente. Nessa situação, a velocidade v2 será igual à metade da velocidade v1.
Em um dia sem vento, um guarda de trânsito encontra-se parado em um cruzamento de uma grande cidade, quando observa a aproximação de uma a ambulância com a sirene ligada emitindo ondas sonoras com frequência de 800 Hz. Porém, devido ao movimento relativo entre a ambulância e ele, o guarda percebe o som emitido pela sirene com uma frequência aparente de 850 Hz.
Considerando que a velocidade do som no ar seja de 340 m/s, a velocidade com que a ambulância se aproxima do guarda é de
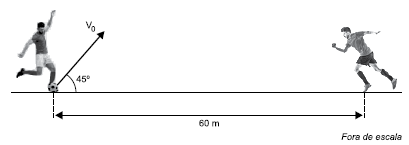
Em um campo de futebol, uma bola é chutada com velocidade inicial v0 = 20 m/s em uma direção que faz 45º com a horizontal. Nesse mesmo instante, um jogador, parado a 60 m do ponto onde ocorreu o chute, começa a correr ao encontro da bola em uma direção contida no mesmo plano vertical que contém a trajetória da bola. Desprezando a resistência do ar e adotando g = 10 m/s2, a velocidade média desse jogador para que ele se encontre com a bola no mesmo instante em que ela atinge o gramado é, aproximadamente,
