Em 1798 o cientista Henry Cavendish realizou uma medida acurada da massa da terra, e, portanto, de sua densidade e mesmo da constante gravitacional ('Experiments to determine the Density of the Earth', Philosophical Transactions of the Royal Society of London, 88 p.469-526, 1798), parâmetro muito importante para o avanço do entendimento geológico de nosso planeta. ,
Nas vizinhanças da Terra, onde altura do corpo em relação ao centro de massa do planeta pode ser aproximada pelo valor do raio da Terra, a igualdade entre a força peso e a Lei da Gravitação Universal de Newton permite associar o valor da aceleração da gravidade g com a constante da gravitação universal G=6,7x10-11m3/kg.s2, a massa e o raio da Terra. Considerando g=10m/s2, π=3, e que a Terra é uma esfera de volume V=4πR3/3 com raio médio de cerca de 6400 km, calcule a densidade do planeta. Dos valores abaixo o que mais se aproxima para o valor obtido é:
Os satélites são ditos geoestacionários quando são colocados em uma órbita circular em torno da Terra. Para um observador sobre a sua superfície, o satélite comporta-se como se estivesse fixo em um determinado local no céu. A figura representa quatro possíveis órbitas circulares de satélites em relação ao plano equatorial da Terra. Todas as órbitas com período de 24 horas:
• órbita polar- plano da órbita faz 90° com o plano equatorial;
• órbita inclinada- plano da órbita faz um ângulo maior que 0° e menor que 90° com o plano equatorial;
• órbita equatorial direta- mesmo sentido de rotação da Terra e no plano equatorial;
• órbita equatorial retrógrada- sentido de rotação oposto ao da Terra e no plano equatorial.
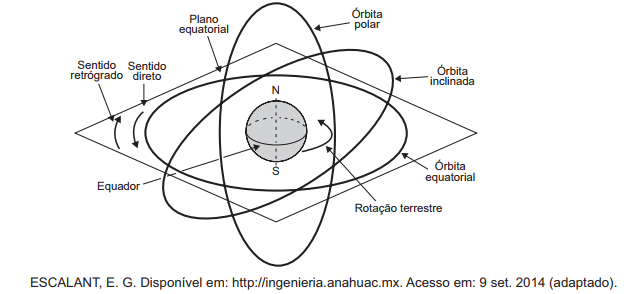
Para que um satélite fique geoestacionário, sua órbita deve ser
Uma nave espacial de massa M é lançada em direção à lua. Quando a distância entre a nave e a lua é de 2,0.108 m, a força de atração entre esses corpos vale F. Quando a distância entre a nave e a lua diminuir para 0,5.108 m, a força de atração entre elas será:
Dois corpos de massas m1 e m2 estão separados por uma distância d e interagem entre si com uma força gravitacional F. Se duplicarmos o valor de m1 e reduzirmos a distância entre os corpos pela metade, a nova força de interação gravitacional entre eles, em função de F, será
As duas figuras a seguir representam, ainda que fora de escala,
alguns astros (pontos brancos, ao fundo) e parte do Sistema
Solar, em dois momentos.
As linhas brancas mais espessas representam a trajetória da luz
envolvendo três astros: Sol, Terra e Júpiter.
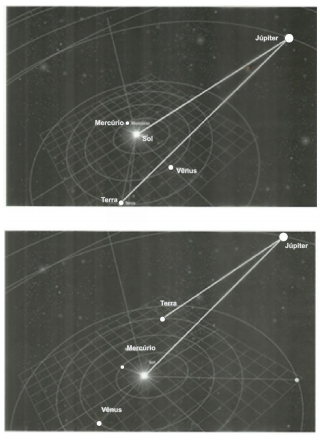
O professor pode utilizar as duas figuras para orientar os alunos
na percepção de que

