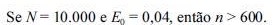Deseja-se fazer uma pesquisa com residentes de uma cidade para determinar que proporção da população gostaria
que o limite de velocidade de uma grande avenida fosse aumentado de 60 km/h para 70 km/h. Considerando uma
amostragem aleatória simples, qual o número mínimo de residentes que devem ser entrevistados para que os
pesquisadores estejam 99% confiantes de que o erro na estimação dessa proporção seja menor que 0,05?
A variância de um conjunto de dados é 4 m2.
Para o mesmo conjunto de dados foram tomadas mais duas medidas de variabilidade:
a diferença entre o terceiro e o primeiro quartil e o coeficiente de variação.
Esses dois valores caracterizam-se, respectivamente, por
Considere um planejamento amostral para uma população de interesse no qual é feita uma divisão dessa população em grupos idênticos à população alvo, como uma espécie de microcosmos da população, e, em seguida, seleciona-se aleatoriamente um dos grupos e retira-se a amostra do grupo selecionado. A técnica de amostragem descrita acima é definida como:
Um instituto de pesquisa deseja avaliar a preferência do eleitor de um determinado município. Para isso, planeja um levantamento por amostragem aleatória simples. O erro amostral tolerado é de 2%, com 95% de confiança (z = 1,96), para as estimativas. Considerando esses dados, assinale a alternativa que apresenta a quantidade de eleitores que devem ser pesquisados.
Julgue os itens seguintes, relativos às técnicas de amostragem
Considere que um tribunal pretenda pesquisar a respeito do
tempo médio em que processos dos tipos A e B são
solucionados. Nesse cenário, supondo que os processos do tipo
A sejam solucionados quase todos no mesmo tempo
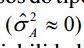
que os do tipo B sejam solucionados com maior variabilidade
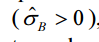
que se escolham n processos de cada tipo e que o B > 0 tamanho amostral seja desprezível com relação ao tamanho
populacional, é correto afirmar que a amostragem estratificada
minimiza a variância da estimativa da média de tempo dos
processos se comparada com a amostragem aleatória simples
com reposição.
Em uma pesquisa eleitoral realizada com 600 eleitores escolhidos aleatoriamente, 360 mostraram-se favoráveis ao candidato X. Deseja-se construir um intervalo de confiança de 95% para a proporção de eleitores favoráveis ao candidato X com base nessa amostra. Para isto, considerou-se normal a distribuição da frequência relativa dos eleitores que são favoráveis ao candidato X, a população de tamanho infinito e que na distribuição normal padrão (Z) a probabilidade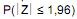 
= 95%. A amplitude deste intervalo é igual a
Se, em determinada fábrica, 10% das peças produzidas são
defeituosas, então, para fins de controle de qualidade, uma
distribuição binomial negativa deve ser usada na situação em que
se deseja calcular a probabilidade de a primeira peça defeituosa ocorrer na décima retirada, no caso de as peças serem retiradas por amostragem aleatória simples com reposição.
Com relação às técnicas de amostragem de populações finitas,
julgue os seguintes itens.
As amostragens aleatórias simples, sistemática, estratificada e por cotas representam planos de amostragem probabilísticos.
No que concerne aos planos amostrais, julgue os itens a seguir.
Considerando uma população finita, de N indivíduos, a média amostral, calculada a partir de amostra de tamanho n < N, é um estimador não viciado para a média populacional tanto no caso de a amostragem aleatória simples ser feita sem reposição quanto no caso em que é feita com reposição.
Na amostragem aleatória simples, a relação entre o tamanho mínimo da amostra - n - e o tamanho da população - N - é dada por n =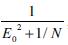 
em que 
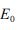representa o erro amostral E 1/ N 1 2 0 + tolerável. Com base nessas informações, julgue os itens seguintes.
