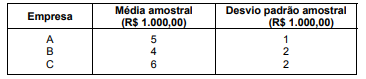
Com base em uma amostra aleatória simples de tamanho n = 16 retirada de uma população normal com média desconhecida μ e variância a2= 9, deseja-se testar a hipótese nula H1: μ = 0 contra a hipótese alternativa H0: μ ≠ 0 por meio da estatística 
, na qual 
denota a média amostral.
Com respeito a esse teste de hipóteses, julgue o item a seguir, sabendo que o valor da média amostral observado na amostra foi igual a 1 e que, relativo a esse teste, o P-valor foi igual a 0,18.
O P-valor é uma medida que representa a potência do teste em tela.
Um determinado ramo de atividade é composto por 3 empresas (A, B e C) independentes. Um estudo é realizado para comparar os salários, em R$ 1.000,00, dos empregados de A, B e C, sabendo-se que não existe alguém trabalhando em mais de uma empresa. Uma amostra aleatória, com reposição, de 24 empregados, sendo 8 de cada uma das empresas citadas, foi retirada da população de empregados desse ramo de atividade. Na tabela abaixo, verifica-se os salários médios e os respectivos desvios padrões amostrais (obtidos por meio de estimadores não viciados das variâncias populacionais) observados para cada uma das amostras.
Se k é o valor da estatística F (F calculado) utilizado para testar a igualdade das médias populacionais dos salários dos empregados em A, B e C obtém-se que
Os estimadores independentes e não viesados E 1, E2 e E3 são utilizados para a média μ de uma população normalmente distribuída e desvio padrão igual a 0,5. Tem-se que E1 = mX1 + nX2 − 2pX3, E2 = mX1 + 2nX2 − 4pX3 e E3 = 2mX1 + nX2 − 3pX3 sendo (X1, X2, X3) uma amostra aleatória simples com reposição da população e m, n e p parâmetros reais tal que n=2m=2p. Entre esses 3 estimadores, o mais eficiente apresenta uma variância igual a
Uma amostra aleatória simples
Y1, Y2,..., Yn, retirada de uma população Bernoulli, é tal que
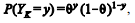
para
y = 0 ou 1, 0 < θ < 1 e k = 1, 2, ..., n. O objetivo é efetuar inferências acerca do parâmetro θ mediante aplicação de métodos computacionais.
Considerando que para
, 
represente a estimativa de θ obtida na r-ésima iteração de um algoritmo de estimação, julgue o seguinte item.
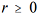
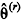
O amostrador de Gibbs, um algoritmo sequencial de Monte Carlo, permite simular a distribuição a priori do parâmetro θ, desde que a forma funcional da sua função de densidade, ƒ(θ), seja conhecida.
Considere uma amostragem aleatória simples de uma população de tamanho muito grande. O tamanho aproximado da amostra que permite estimar uma proporção Y, com margem de erro máxima de 0,05, a um nível de confiança de 90%, é
Os tempos de duração de exames de cateterismo cardíaco ( Y, em minutos) efetuados por determinada equipe médica seguem uma distribuição normal com média µ e desvio padrão σ, ambos desconhecidos. Em uma amostra aleatória simples de 16 tempos de duração desse tipo de exame, observou-se tempo médio amostral igual a 58 minutos, e desvio padrão amostral igual a 4 minutos.
A partir da situação hipotética apresentada e considerando Φ(2) = 0,977, em que Φ(z) representa a função de distribuição acumulada de uma distribuição normal padrão e z é um desvio padronizado, julgue o item que se segue, com relação ao teste de hipóteses H0 = µ ≥ 60 minutos, contra HA = µ < 60 minutos, em que H0 e HA denotam, respectivamente, as hipóteses nula e alternativa.
Nesse teste de hipóteses, comete-se o erro do tipo II caso a hipótese H0 seja rejeitada, quando, na verdade, H0 não deveria ser rejeitada.
X1, X2, ..., X10 representa uma amostra aleatória simples retirada de uma distribuição normal com média µ e variância σ2, ambas desconhecidas. Considerando que 
e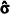 
representam os respectivos estimadores de máxima verossimilhança desses parâmetros populacionais, julgue o item subsecutivo.
A soma X1 + X2 + ... + X10 é uma estatística suficiente para a estimação do parâmetro μ.
Uma amostra aleatória simples
Y1, Y2,..., Yn, retirada de uma população Bernoulli, é tal que
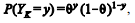
para
y = 0 ou 1, 0 < θ < 1 e k = 1, 2, ..., n. O objetivo é efetuar inferências acerca do parâmetro θ mediante aplicação de métodos computacionais.
Considerando que para
, represente a estimativa de θ obtida na r-ésima iteração de um algoritmo de estimação, julgue o seguinte item.
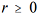
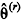
No algoritmo de Metropolis-Hastings tem-se a forma iterativa
, na qual ƒ representa a função de densidade a priori de θ, e 
> 0 representa um incremento aleatório. Nesse algoritmo, a probabilidade de aceitação do valor proposto 
como uma estimativa viável para o parâmetro de interesse é constante.
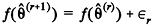
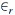
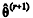
Uma amostra aleatória simples
Y1, Y2,..., Yn, retirada de uma população Bernoulli, é tal que
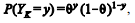
para
y = 0 ou 1, 0 < θ < 1 e k = 1, 2, ..., n. O objetivo é efetuar inferências acerca do parâmetro θ mediante aplicação de métodos computacionais.
Considerando que para
, represente a estimativa de θ obtida na r-ésima iteração de um algoritmo de estimação, julgue o seguinte item.
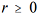
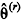
O método de Monte Carlo via cadeia de Markov (MCMC) pertence à classe de algoritmos de estimação não sequencial, em que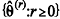 
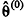
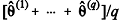
forma um conjunto de valores mutuamente independentes. Excluindo-se o valor inicial 
, uma estimativa do parâmetro θ é dada por 
, na qual q representa um valor suficientemente grande.
Deseja-se estimar o total de carboidratos existentes em um lote de 500.000 g de macarrão integral. Para esse fim, foi retirada uma amostra aleatória simples constituída por 5 pequenas porções desse lote, conforme a tabela seguinte, que mostra a quantidade x amostrada, em gramas, e a quantidade de carboidratos encontrada, y, em gramas.
Com base nas informações e na tabela apresentadas, julgue o item a seguir.
Considerando o estimador de razão, estima-se que existem 250.000 g de carboidratos nesse lote de macarrão integral.
Suponha que o tribunal de contas de determinado estado disponha de 30 dias para analisar as contas de 800 contratos firmados pela administração. Considerando que essa análise é necessária para que a administração pública possa programar o orçamento do próximo ano e que o resultado da análise deve ser a aprovação ou rejeição das contas, julgue os itens a seguir. Sempre que necessário, utilize que P(Z > 1,96) = 0,025 e P(Z > 1,645) = 0,05, em que Z representa a variável normal padronizada.
Caso se opte por uma amostra aleatória estratificada, a variância da média amostral será menor ou igual à que seria obtida por amostragem aleatória simples.
Um prefeito acredita que os habitantes de seu município estão lendo pouco, pois a biblioteca municipal está sempre
com pouco movimento. Para mudar essa situação, ele pensou em fazer uma campanha para estimular a leitura,
entretanto precisa comprovar estatisticamente que a média de livros lidos por habitante do município está abaixo da
média nacional para conseguir a liberação da verba para executar a campanha.
Informações adicionais
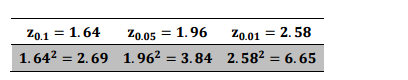
Qual o tamanho da amostra que o prefeito precisa coletar usando amostragem aleatória simples se ele deseja ter
90% de confiança e margem de erro 1, sabendo através de um estudo prévio que σ2
Suponha que o tribunal de contas de determinado estado disponha de 30 dias para analisar as contas de 800 contratos firmados pela administração. Considerando que essa análise é necessária para que a administração pública possa programar o orçamento do próximo ano e que o resultado da análise deve ser a aprovação ou rejeição das contas, julgue os itens a seguir. Sempre que necessário, utilize que P(Z > 1,96) = 0,025 e P(Z > 1,645) = 0,05, em que Z representa a variável normal padronizada.
Se a lista de contratos estiver ordenada pela data de assinatura, o resultado de uma amostra sistemática será similar ao de uma amostra selecionada por amostragem aleatória simples.
Considerando uma população finita em que a média da variável de
interesse seja desconhecida, julgue os itens a seguir.
Em uma amostragem aleatória simples, sem reposição das observações selecionadas no conjunto de observações para sorteio, a amostra final resultante apresenta dependência entre os valores amostrados.
Com relação às técnicas de amostragem, julgue os itens
subsequentes.
Na amostragem aleatória simples sem reposição (AASs), o
tamanho amostral n é calculado por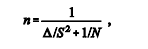
em que N é o tamanho da população, S2 é a variância amostral
e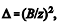 
sendo B o erro máximo de estimação e z o quantil
da distribuição normal. Dessa forma, é correto afirmar que o
maior tamanho amostral na AASs será menor que N.
