Do grupo dos 6 novos policiais de uma delegacia, 2 deles serão escolhidos para um treinamento especial.
O número de pares diferentes de policiais que podem ser enviados para o treinamento especial é:
A quantidade de retângulos com lados de comprimento inteiro
que é possível formar, tendo sempre um perímetro de 24 cm, é
O retângulo ABCD da figura a seguir tem as dimensões AB = 10 e BC = 6.
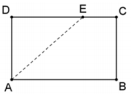
O ponto E do lado CD é tal que o segmento AE divide o retângulo em duas partes de forma que a área de uma seja o dobro da área da outra.
O segmento DE mede
A figura a seguir mostra a quadra retangular ABCD de um quartel, com 30 m de comprimento e 21 m de largura, dividida em quadrados iguais.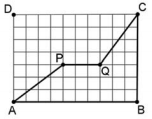
Dois soldados, Pedro e Paulo, caminharam de A até C por caminhos diferentes: Pedro percorreu os lados AB e BC, e Paulo percorreu os segmentos AP, PQ e QC.
É correto concluir que
As figuras a seguir foram construídas sobre papel quadriculado.
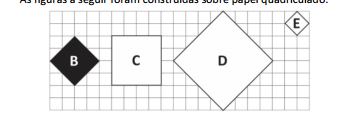
Sobre as figuras B, C, D e E, assinale a afirmativa correta.
Um jogo de dados tem por objetivo obter as somas de 1 a 9,
sendo que o jogador pode escolher, em cada jogada, se vai lançar
um dado apenas ou os dois dados. Os participantes vão se
revezando no lançamento de dados e, quem conseguir todos
aqueles totais em primeiro lugar, e em qualquer ordem, será o
vencedor.
Sobre as chances de conseguir determinadas somas, é correto
afirmar que
As figuras a seguir representam 2 canteiros que serão cercados e
onde serão plantadas mudas de flores.
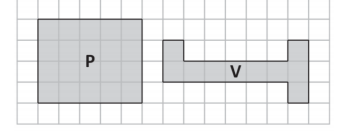
Dentre as ponderações do dono listadas a seguir, assinale a que
afirma motivo correto para a decisão.
O piso de uma sala é representado pelo polígono da figura abaixo, onde dois lados consecutivos são sempre perpendiculares. As medidas indicadas na figura estão em metros.
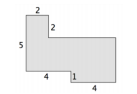
A área dessa sala, em metros quadrados, é:
Uma fatura de cartão de crédito foi paga com dois meses de atraso, e o valor pago, incluindo os 25% de juros correspondentes ao bimestre, foi de R$ 1100,00.
O valor da fatura sem os juros era de
João tem hoje 22 anos e lembrou que, há oito anos, nesse mesmo dia do ano, sua irmã Maria disse para ele: “Eu tenho a metade da sua idade”.
Nesse mesmo dia do ano, quando Maria tiver 35 anos, João terá:
Suponha que, de um baralho normal, contendo 52 cartas de
quatro naipes, é extraído, sem reposição e aleatoriamente, um
total de quatro cartas. Se a carta “Ás" é equivalente a uma figura
(ou seja, são 4 figuras e 9 números de cada naipe), é correto
afirmar que a probabilidade de que todas sejam:
A figura a seguir mostra o gráfico da função f(x) = log2x e os pontos:
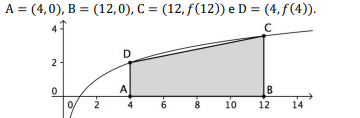
Considerando f(3) = 1,585, a área do quadrilátero ABCD é igual a
A seguir estão escritas algumas letras do alfabeto grego básico.
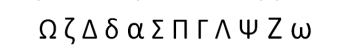
Sobre essas letras, analise as afirmativas a seguir.
I. Todas são linhas poligonais.
II. Algumas são linhas abertas simples.
III. Apenas uma é uma linha poligonal fechada.
IV. Algumas são poligonais abertas.
V. Todas são linhas não-simples.
Está correto o que se afirma em
A figura abaixo mostra um retângulo de 5 por 2.
Juntando três retângulos iguais a esse, foi formada a figura abaixo.
A medida do contorno dessa figura é igual a:
Para trabalhar um conceito ainda pouco conhecido por seus
alunos, o professor exibiu contraexemplos relacionando
características de alguns polígonos. Para isso, preparou o
seguinte exercício para seus alunos:
Observe as figuras a seguir.
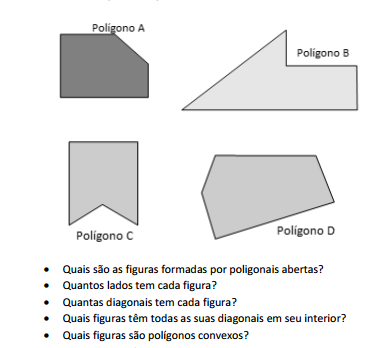
Essa questão envolveu os seguintes conceitos:
Helena entra em uma sorveteria que oferece sorvetes de 8 sabores diferentes. Helena deseja escolher uma casquinha com duas bolas de sorvete não necessariamente de sabores diferentes. A ordem em que as bolas forem colocadas na casquinha não fará a escolha de Helena ser diferente.
O número de maneiras de Helena escolher sua casquinha é
Considere todas as senhas formadas por três vogais maiúsculas. São exemplos dessas senhas: EEE, OIA e UAU.
Dentre todas as senhas desse tipo, escolhendo ao acaso uma delas, a probabilidade de que ela tenha duas letras iguais e uma diferente é de