Aprova Concursos - Simulado Express

O Ministério da Educação in Jacobsen, Cruz Junior e Moretto Neto (2006), expõe certas habilidades que o aluno de Administração precisa desenvolver e, dentre elas, é apresentada a negociação, cuja definição é

a) propor e implementar modelos de gestão, inovar e demonstrar um espírito empreendedor.

b) propor e implementar atitudes flexíveis e de adaptação, e demonstrar um espírito empreendedor.

c) demonstrar atitudes flexíveis e de inovação, além de trabalhar em equipes diversas.

d) demonstrar atitudes inovadoras e de adaptação ao ambiente externo.

e) demonstrar atitudes flexíveis e de adaptação a terceiros e a situações diversas.

Uma estrutura organizacional é uma forma de atribuir tarefas e de especializar os blocos de trabalho da organização. Assinale a alternativa que apresenta a base utilizada no processo de organizar as tarefas em blocos de trabalho.

a) Critérios de descentralização.

b) Critérios de terceirização.

c) Critérios de delegação.

d) Critérios de departamentalização.

e) Critérios de diferenciação.

A gestão por processos ou administração por processos é uma importante tendência organizacional cujo resultado é

a) uma estrutura vertical de processos criada pela cadeia de comando.

b) uma cadeia de valor em cada departamento e seus processos.

c) uma cadeia formada pelos dirigentes com os processos.

d) uma cadeia horizontal de processos interligados.

e) uma estrutura com departamentalização independente.

Os números de processos autuados em duas repartições públicas (R1 e R2) independentes, durante 40 dias, estão representados na tabela abaixo, sendo m e n inteiros positivos.

Calculando a soma da média aritmética (número de processos por dia) com a moda e com a mediana de cada repartição, verifica-se que a soma obtida na repartição R2 supera a soma obtida na repartição R1 em

a) 2,05

b) 0,55

c) 1,05

d) 1,30

e) 1,55

A tabela a seguir apresenta a distribuição de frequências dos salários, em número de salários mínimos (SM), dos funcionários de um órgão público:

Sabe-se que:

b - a = 5%,

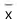
é a média salarial, obtida por meio dessa tabela, calculada como se todos os valores de cada faixa salarial coincidissem com o ponto médio da referida faixa,

md é a mediana salarial, calculada por meio dessa tabela pelo método da interpolação linear.

Nessas condições, 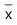+ md, em anos, é igual a

9,85

11,35

11,05

10 ,95

11 ,65

A empresa Sigma apresenta pela tabela abaixo a distribuição dos salários registrados de seus 100 empregados em reais.

Não foram fornecidos os números de empregados que ganham R$ 10.000,00 e R$ 15.000,00 (denotados na tabela por x e y, respectivamente), mas sabe-se que a média aritmética dos salários é igual a R$ 8.400,00. O valor da soma da respectiva moda e da respectiva mediana desses salários é, em reais, igual a

a) 625y.

b) 1.000y.

c) 750y.

d) 500y.

e) 600y.

Uma população é formada pelos salários dos empregados de uma empresa. Decide-se dar um aumento de 10% sobre todos os salários mais um adicional fixo de R$ 500,00 para todos os salários. Com relação às medidas de tendência central e de dispersão é correto afirmar que a nova população formada terá

a) um desvio padrão igual ao desvio padrão da população anterior multiplicado por 1,10 acrescido de R$ 500,00.

uma variância igual à variância da população anterior multiplicada por 1,21 acrescida de 250.000 (R$)².

c) uma média aritmética igual à média aritmética da população anterior acrescida de R$ 500,00.

d) uma mediana igual à mediana da população anterior acrescida de R$ 500,00.

e) um desvio padrão igual ao desvio padrão da população anterior multiplicado por 1,10 e uma variância igual à variância da população anterior multiplicada por 1,21.

A tabela a seguir apresenta a distribuição de frequências dos salários, em número de salários mínimos (SM), dos funcionários de um órgão público:

Sabe-se que:

b - a = 5%,

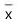
é a média salarial, obtida por meio dessa tabela, calculada como se todos os valores de cada faixa salarial coincidissem com o ponto médio da referida faixa,

md é a mediana salarial, calculada por meio dessa tabela pelo método da interpolação linear.

Nessas condições, 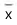+ md, em anos, é igual a

9,85

11,35

11 ,05

10,95

11,65

Considere que o Estado esteja enfrentando dificuldade financeira, em função da queda de arrecadação de impostos, para honrar suas obrigações perante a SPPREV em relação à insuficiência financeira dos Regimes Previdenciários Próprios dos Servidores – RPPS administrados pela Autarquia. Aventou-se, como forma de obtenção de receita extraordinária para cobertura de tal déficit, a possibilidade de alienação de imóveis de propriedade do Estado e a destinação do produto da venda à tal finalidade. De acordo com as disposições da Lei de Responsabilidade Fiscal − LRF (Lei Complementar nº 101/2000), tal destinação afigurase juridicamente

a) viável, se tal destinação constar de lei, configurando exceção à regra que veda aplicação de receita de capital a despesas correntes (de pessoal e custeio).

b) inviável, por configurar violação à denominada “regra de ouro”, que proíbe cobertura de quaisquer despesas correntes com recursos provenientes da alienação de bens de capital.

c) viável, desde que adotado o modelo de capitalização e o produto da alienação dos imóveis seja destinado a fundo de previdência complementar constituído para tal finalidade.

d) viável apenas para cobertura das contribuições correntes do Estado ao RPPS, vedada a destinação para cobertura de insuficiências financeiras ou atuariais.

e) inviável, eis que a LRF admite, como exceção à denominada “regra de ouro”, a destinação de receitas de capital apenas para cobertura de obrigações do Estado junto à União, incluídas aquelas perante o Regime Geral de Previdência Social.

A Lei Orçamentária Anual, para o exercício de 2017, do Estado de Altamira do Norte, foi publicada em 30/12/2016. No que tange a execução orçamentária e o cumprimento de metas, segundo a Lei Complementar no 101/2000, a programação financeira e o cronograma de execução mensal de desembolso será estabelecida

a) pelo controle interno, até 30 dias após a publicação do orçamento.

b) por cada um dos Poderes, até 45 dias após a publicação do orçamento.

c) pelo Poder Executivo, até 30 dias após a publicação do orçamento.

d) pela Administração direta e indireta, até 30 dias após o início da execução orçamentária.

e) pelo Poder Executivo, até 30 dias após o início da execução orçamentária.

Um dos instrumentos introduzidos pela Lei de Responsabilidade Fiscal, dentro do escopo da gestão fiscal responsável, é o denominado Anexo de Metas Fiscais, o qual integra, obrigatoriamente,

a Lei de Diretrizes Orçamentárias, englobando metas de receitas, despesas, resultados nominal e primário e montante da dívida pública, para o exercício a que se referirem e para os dois seguintes.

o Plano Plurianual, sendo elaborado juntamente com este, a cada 4 anos, e referindo-se à projeção de receitas e despesas dos 5 exercícios subsequentes.

a Lei Orçamentária Anual, descrevendo, de forma pormenorizada, as receitas tributárias e não tributárias do exercício correspondente.

o Decreto de Execução Orçamentária, sendo editado juntamente com tal diploma para fins de ajustar as estimativas consignadas na Lei Orçamentária Anual.

os relatórios quadrimestrais que devem ser editados no curso da execução orçamentária, sendo elaborados e aprovados juntamente com o primeiro relatório encaminhado ao Tribunal de Contas do Estado.

Suponha que, em função do fechamento de diversas indústrias e forte queda de arrecadação de impostos, o Estado tenha decidido adotar medidas de redução de despesas e de aumento de receitas extraordinárias, especialmente com a alienação de imóveis de sua titularidade. Considerando as disposições da Lei de Responsabilidade Fiscal relativas à gestão financeira e patrimonial,

as medidas voltadas à obtenção de receitas extraordinárias somente poderão ser implementadas após esgotadas as de redução de despesas correntes.

as receitas obtidas com a alienação de imóveis não poderão ser aplicadas em despesas correntes, salvo se destinadas por lei a regime de previdência geral e próprio dos servidores.

as receitas obtidas com alienação de imóveis devem ser aplicadas prioritariamente no pagamento de folha de pagamento de pessoal ativo e nos proventos de inativos e pensionistas.

o Estado poderá paralisar o pagamento de dívida pública junto à União se as medidas adotadas não forem suficientes para a cobertura de suas despesas correntes.

a aplicação dos recursos obtidos com alienação de imóveis em despesas de pessoal somente estará autorizada se ainda não atingido o limite prudencial de gastos.

De acordo com a disciplina estabelecida pela Lei de Responsabilidade Fiscal para dívida e endividamento dos entes públicos,

a) é vedada a aquisição, por Estados e Municípios, bem como por entidades integrantes da Administração indireta de ambos, de títulos da dívida pública emitidos pela União.

b) são expressamente vedadas operações de crédito por Antecipação de Receita Orçamentária – AROs.

c) as operações de crédito contraídas por Estados devem, obrigatoriamente, contar com contragarantia da União.

d) é vedada a concessão de garantia a operações de crédito contraídas por Municípios, inclusive mediante vinculação do produto da participação nos impostos estaduais.

e) integram a dívida consolidada os precatórios judiciais não pagos durante a execução do orçamento em que foram incluídos.

Um político ou um servidor utiliza sua verba de representação ou cartão corporativo em negócios não previstos à sua condição de pessoa pública ou do exercício profissional. Com base nestas informações, os princípios de administração pública atingidos são:

a) Legalidade e Publicidade.

b) Moralidade e Legalidade.

c) Publicidade e Finalidade.

d) Moralidade e Impessoalidade.

e) Impessoalidade e Publicidade.

Uma das definições para o conceito de ética corresponde ao “conjunto de princípios morais que devem ser respeitados no exercício de uma profissão”. Nesse sentido, a ética na Administração Pública, considerando o regime próprio a que se submete,

a) traduz-se na observância do princípio da legalidade.

b) corresponde ao conceito de probidade administrativa.

c) significa a busca do interesse público, ainda que em detrimento da legalidade em seu sentido estrito.

d) impõe o sigilo na atuação do servidor público e o zelo na administração de recursos públicos.

e) envolve, entre outros aspectos, a legalidade, a moralidade e a eficiência na atuação do agente público.