Em um jogo, os jogadores escolhem três números inteiros diferentes, de 1 a 10. Dois números são sorteados e se ambos estiverem entre os três números escolhidos por um jogador, então ele ganha um prêmio. O sorteio é feito utilizando-se uma urna com 10 bolas numeradas, de 1 até 10, e consiste na retirada de duas bolas da urna, de uma só vez, seguida da leitura em voz alta dos números nelas presentes.

Qual é a probabilidade de um jogador ganhar um prêmio no sorteio do jogo?

A relação do cliente com o sistema bancário tradicional vem passando por transformações nos últimos cincos anos com o crescimento dos bancos digitais. Analisar o perfil dos clientes dos bancos digitais, considerando idade, classe social, renda e motivação, é uma tarefa importante para os bancos tradicionais com o objetivo de preservar a posição de principal Banco na relação com o Cliente.
Para tal fim, uma agência bancária analisou os seguintes dados de uma pesquisa amostral sobre bancos digitais:

Escolhendo-se ao acaso um dos entrevistados dessa pesquisa, qual é, aproximadamente, a probabilidade de esse cliente ter um relacionamento com banco digital e de ter apresentado como motivo para iniciar esse relacionamento a facilidade de poder resolver tudo pela internet?

Os alunos de certa escola formaram um grupo de ajuda humanitária e resolveram arrecadar fundos para comprar alimentos não perecíveis. Decidiram, então, fazer uma rifa e venderam 200 tíquetes, numerados de 1 a 200. Uma funcionária da escola resolveu ajudar e comprou 5 tíquetes. Seus números eram 75, 76, 77, 78 e 79. No dia do sorteio da rifa, antes de revelarem o ganhador do prêmio, anunciaram que o número do tíquete sorteado era par.

Considerando essa informação, a funcionária concluiu acertadamente que a probabilidade de ela ser a ganhadora do prêmio era de

Os analistas de uma seguradora estimam corretamente que a probabilidade de um concorrente entrar no mercado de seguro de fiança locatícia é de 30%. É certo que se, de fato, o concorrente entrar no mercado, precisará aumentar seu quadro de funcionários. Sabe-se que, caso o concorrente não pretenda entrar no mercado desse segmento, existem 50% de probabilidade de que ele aumente o quadro de funcionários.

Se o concorrente aumentou o quadro de funcionários, a probabilidade de que ele entre no mercado de seguro de fiança locatícia é de:

Para obter uma amostra de tamanho 1.000 dentre uma população de tamanho 20.000, organizada em um cadastro em que cada elemento está numerado sequencialmente de 1 a 20.000, um pesquisador utilizou o seguinte procedimento:

I - calculou um intervalo de seleção da amostra, dividindo o total da população pelo tamanho da amostra: 20.000/1.000 = 20;

II - sorteou aleatoriamente um número inteiro, do intervalo [1, 20]. O número sorteado foi 15; desse modo, o primeiro elemento selecionado é o 15º;

III - a partir desse ponto, aplica-se o intervalo de seleção da amostra: o segundo elemento selecionado é o 35º (15+20), o terceiro é o 55º (15+40), o quarto é o 75º (15+60), e assim sucessivamente.

O último elemento selecionado nessa amostra é o

Há dez anos a média das idades, em anos completos, de um grupo de 526 pessoas era de 30 anos, com desvio padrão de 8 anos.

Considerando-se que todas as pessoas desse grupo estão vivas, o quociente entre o desvio padrão e a média das idades, em anos completos, hoje, é

Uma pesquisa foi encomendada para saber as condições de funcionamento das escolas de um município. O Gráfico I mostra a distribuição das escolas pelas quantidades de alunos, e o Gráfico II mostra a presença ou não de cantina e ginásio nas escolas com mais de 500 alunos.

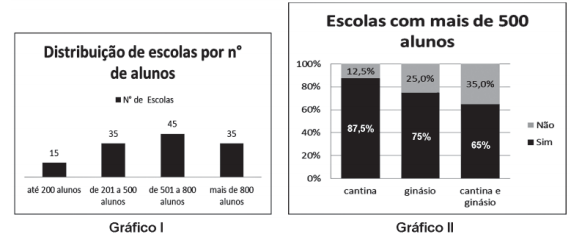
O número de escolas, com mais de 500 alunos, que não possuem cantina nem ginásio é

Dois eventos A e B são tais que A ⊂ B. Avalie se, nesse caso, as afirmativas a seguir estão corretas.

I. P[A] ≤ P[B].

II. P[A|B] = P[A]/P[B].

III. P[B|A] = 1.

Assinale:

Uma urna I contém inicialmente 4 bolas azuis e 6 bolas vermelhas; nessa ocasião, a urna II contém 5 bolas azuis e 4 bolas vermelhas, e a urna III, 2 azuis e 7 vermelhas.

Uma bola é sorteada da urna I e colocada na urna II. Em seguida, uma bola é sorteada da urna II e colocada na urna III. Por fim, uma bola é sorteada da urna III.

A probabilidade de que a bola sorteada da urna III seja azul é igual a

Sabe-se que a probabilidade de condenação em 1ª instância, para certo juízo, é igual a 1/5, enquanto a probabilidade de que a decisão seja alterada por um recurso é igual a 1/3.

Se, em qualquer caso, as partes estão dispostas a recorrer até a 3ª instância, a probabilidade de que haja uma absolvição é:

Seja X uma variável aleatória discreta cuja função distribuição de probabilidade acumulada é dada por:

Como consequência, é correto afirmar que:

10% das lâmpadas fabricadas pela empresa A queimam antes de 1000h de funcionamento. Das fabricadas pela empresa B, 5% queima antes de 1000h de funcionamento. Das fabricadas pela empresa C, 1% queima antes de 1000h de funcionamento. Em uma grande loja de varejo, 20% das lâmpadas em estoque são da marca A, 30% são da marca B e 50% são da marca C.

Uma lâmpada é escolhida ao acaso do estoque dessa loja. A probabilidade de que ela não queime antes de 1000h de funcionamento é igual a

Sobre as vantagens da amostragem por conglomerados, avalie as afirmativas a seguir.

I. O plano amostral é mais eficiente já que dentro dos conglomerados os elementos tendem a ser mais parecidos.

II. Não há necessidade de uma lista de identificação dos elementos da população.

III. Tem, em geral, menor custo por elemento, principalmente quando o custo por observação cresce se aumenta a distância entre os elementos.

Está correto o que se afirma em

A tabela a seguir mostra o número de gols sofridos por um time de futebol nas dez primeiras partidas de um campeonato:

A média e a mediana do número de gols sofridos nesses jogos são respectivamente