Na guerra do Golfo, em janeiro de 1991, as forças iraquianas abriram as válvulas de poços de petróleo e oleodutos ao se retirarem do Kuwait. O volume de petróleo despejado foi estimado em 770 piscinas olímpicas, causando o maior vazamento deliberado de petróleo da história.

Sobre esse desastre ambiental, considere as seguintes relações:

• Cada piscina olímpica tem 50 metros de comprimento, 25 metros de largura e 2 metros de profundidade.

• 1 m³ equivale a 1000 litros;

• 1 barril de petróleo cru estadunidense (US bbl oil) corresponde a, aproximadamente, 159 litros.

Qual foi a quantidade estimada, em barris de petróleo, que foi despejada no Golfo Pérsico naquela ocasião?

Durante um atendimento, o cliente de um banco relata ao gerente de atendimento sua disponibilidade para investir R$400.000,00. O gerente tem ao seu dispor 5 opções de investimento: renda fixa, CDB, fundo de ações, LCI e LCA. Ao cliente foi oferecida uma carteira diversificada de
20%, 10%, 30%, 15% e 25%, respectivamente.

Sendo assim, verifica-se que o valor sugerido para

Sejam A e B duas matrizes quadradas 2x2, tal que 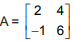, e A^.B = I, onde I é a matriz identidade 2x2.

Assim, a soma dos elementos da matriz B é igual a

Uma sequência numérica tem seu termo geral representado por a_n, para n ≥ 1. Sabe-se que a₁ = 0 e que a sequência cujo termo geral é b_n = a_n+1 - a_n, n ≥ 1, é uma progressão aritmética cujo primeiro termo é b₁ = 9 e cuja razão é igual a 4.

O termo a₁₀₀₀ é igual a

O quarto, o quinto e o sexto termos de uma progressão aritmética são expressos por x + 1, x² + 4 e 2x² + 3, respectivamente.

A soma dos dez primeiros termos dessa progressão aritmética é igual a

Considere a sequência numérica cujo termo geral é dado por a_n=2^1-3n, para n ≥ 1.

Essa sequência numérica é uma progressão

A soma dos n primeiros termos de uma progressão geométrica é dada por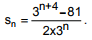

Quanto vale o quarto termo dessa progressão geométrica?