Na matriz A =  , m, n e p são números inteiros ímpares consecutivos tais que m < n < p.
, m, n e p são números inteiros ímpares consecutivos tais que m < n < p.
O valor de  é
é
Sejam A e B duas matrizes quadradas 2x2, tal que 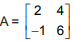
Assim, a soma dos elementos da matriz B é igual a
Considere uma progressão aritmética, em que a8 = a2 + a6, e a soma dos 10 primeiros termos dessa sequência é igual a 330.
Assim, a razão dessa progressão é igual a
O quarto, o quinto e o sexto termos de uma progressão aritmética são expressos por x + 1, x2 + 4 e 2x2 + 3, respectivamente.
A soma dos dez primeiros termos dessa progressão aritmética é igual a
Uma sequência numérica tem seu termo geral representado por an, para n ≥ 1. Sabe-se que a1 = 0 e que a sequência cujo termo geral é bn = an+1 - an, n ≥ 1, é uma progressão aritmética cujo primeiro termo é b1 = 9 e cuja razão é igual a 4.
O termo a1000 é igual a
O número de equipamentos vendidos por uma empresa vem aumentando a uma taxa de crescimento constante nos últimos anos, conforme mostra a Tabela a seguir.
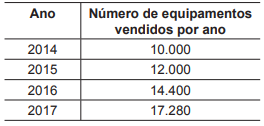
A empresa precisa programar-se para que sua produção possa atender às demandas futuras, caso essa tendência se mantenha.
Assim, considerando-se 2,5 como aproximação para 1,25, e mantida a taxa de crescimento observada, o número mais próximo para a previsão de vendas de todo o período de 2014 a 2023, em milhares de equipamentos, contando, inclusive, com as vendas de 2014 e 2023, é igual a
Considere a sequência numérica cujo termo geral é dado por an=21-3n, para n ≥ 1.
Essa sequência numérica é uma progressão
Para x > 0, seja Sx a soma
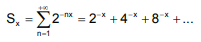
O número real x para o qual se tem 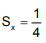 é
é